课程 图形学 Animation

about 图形学中的动画效果，只讨论 Physics-Based Animation。

属于图形学系列文章。

Type of Dynamics:

• Point (particle)
• Rigid body
• Deformable body (e.g., elastic materials, fluids, smoke)

Physics-Based Animation

定义：Simulating object motion

Q：How to simulate?

A：Simulating the underlying physics

Q：What is the simulation like?

A：一般通过 (ordinary or partial) differential equations 来描述

例子：

其中：

$x\left(t\right)$: a moving point

$\dot{x}\left(t\right)$: its velocity

The differential equation $\dot{x}\left(t\right)=f(x,t)$ defines a vector field over x (at any time t)

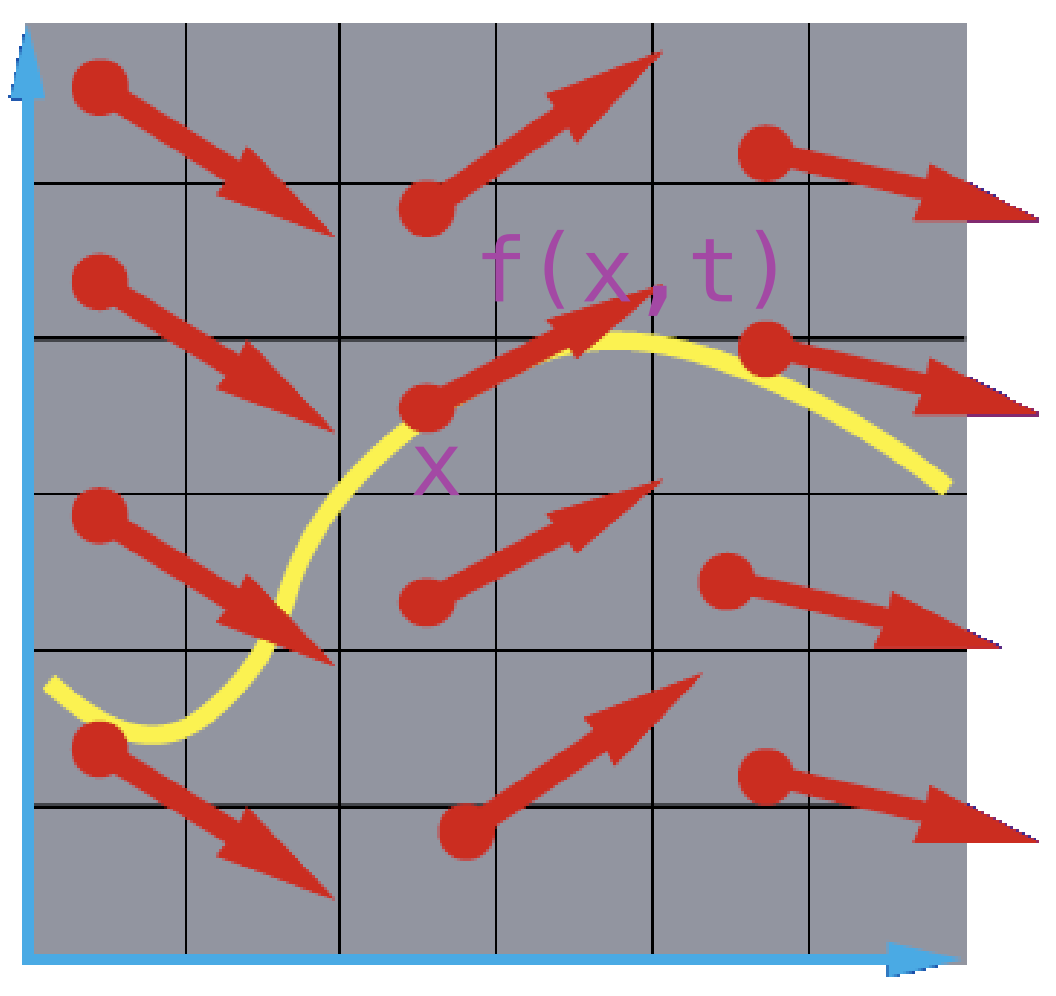
Integral Curves: 图中黄色的曲线

Initial Value Problems: 给定函数的微分方程和其中的一个点，求原函数是什么

介绍了Euler’s Method求解这个问题

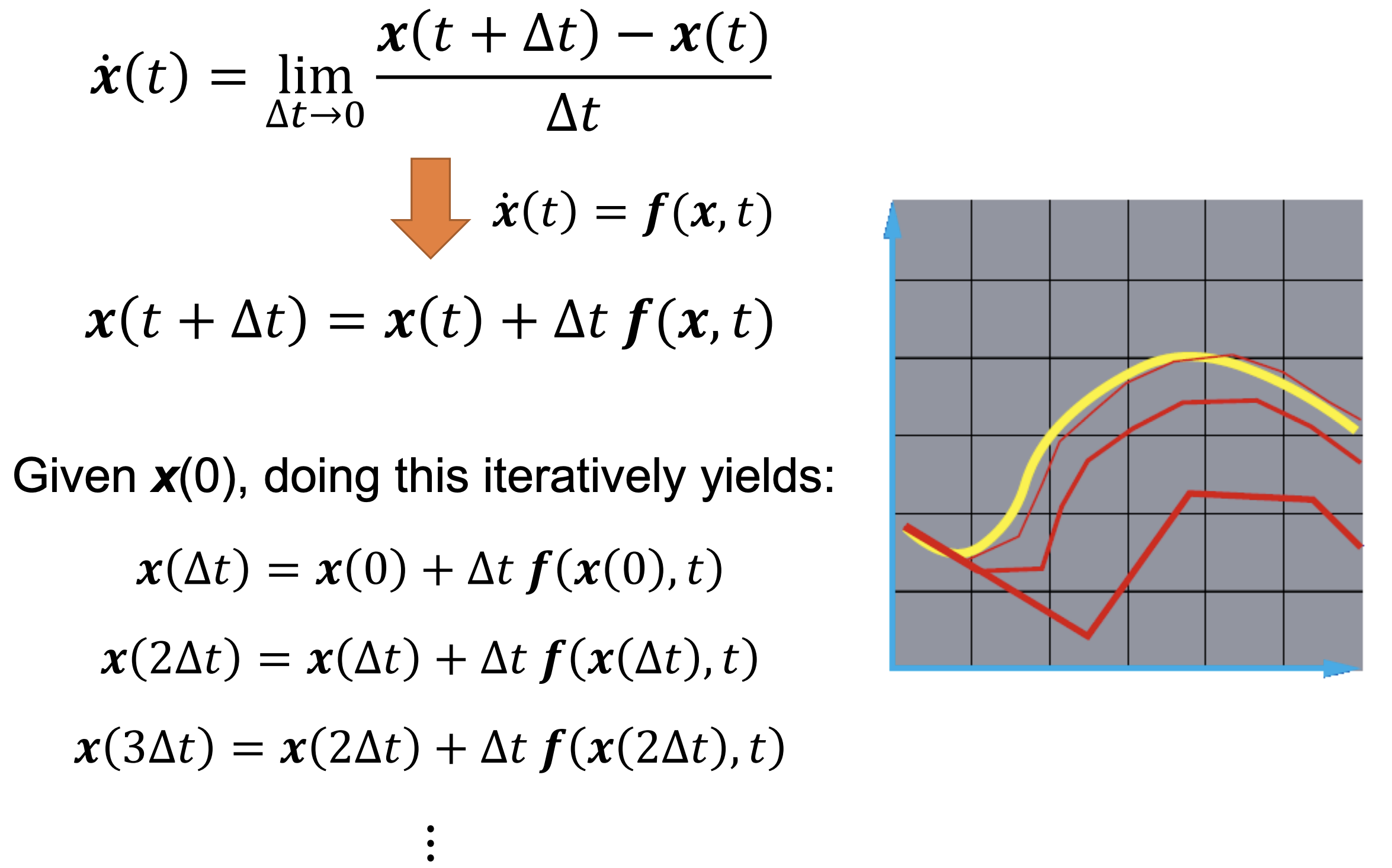
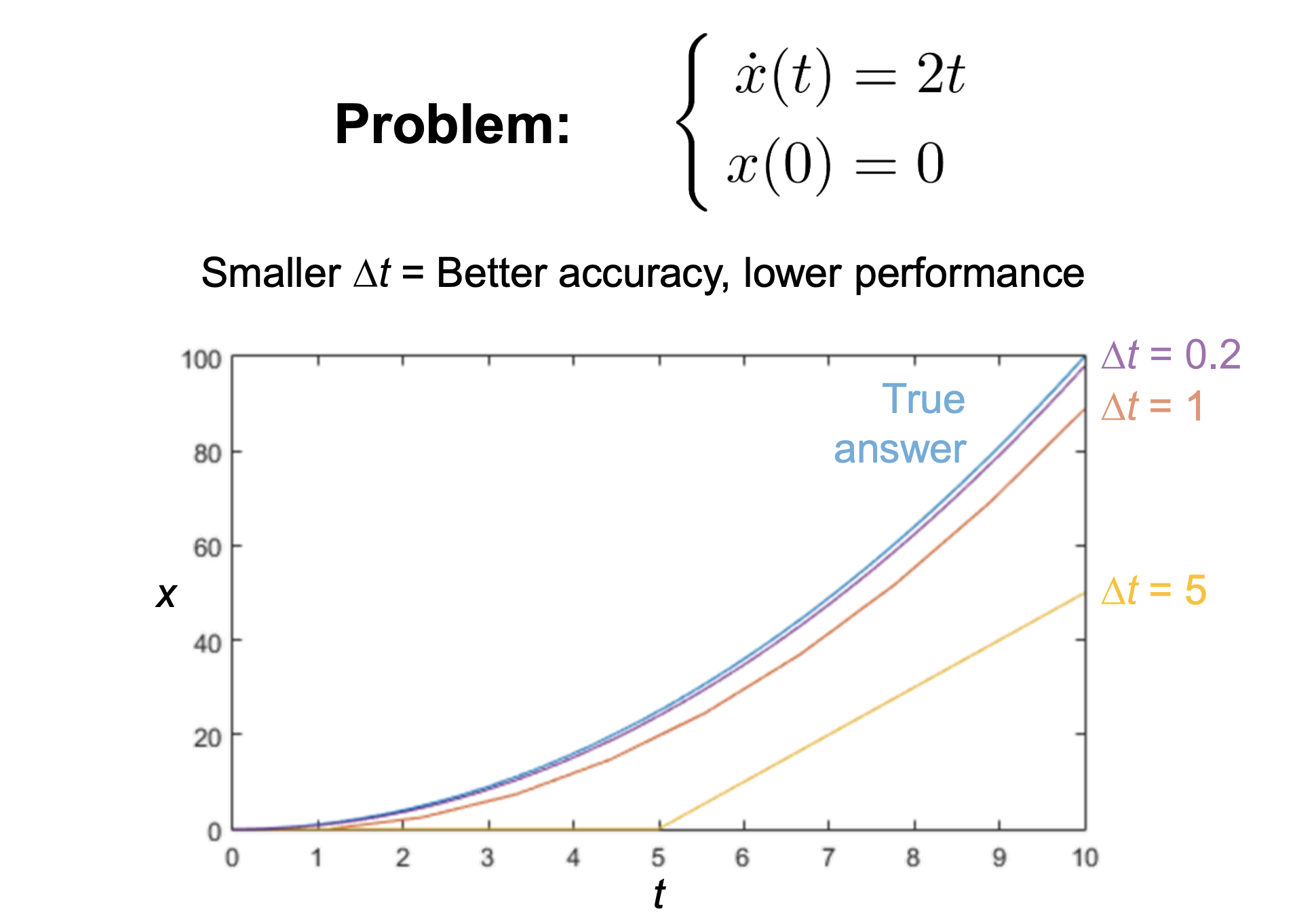
但是这方法有很多问题

Problem 1: Inaccuracy 误差会导致x(t)从一个圆圈变成有明显棱角的螺线

Problem 2: Instability 下图来自维基百科

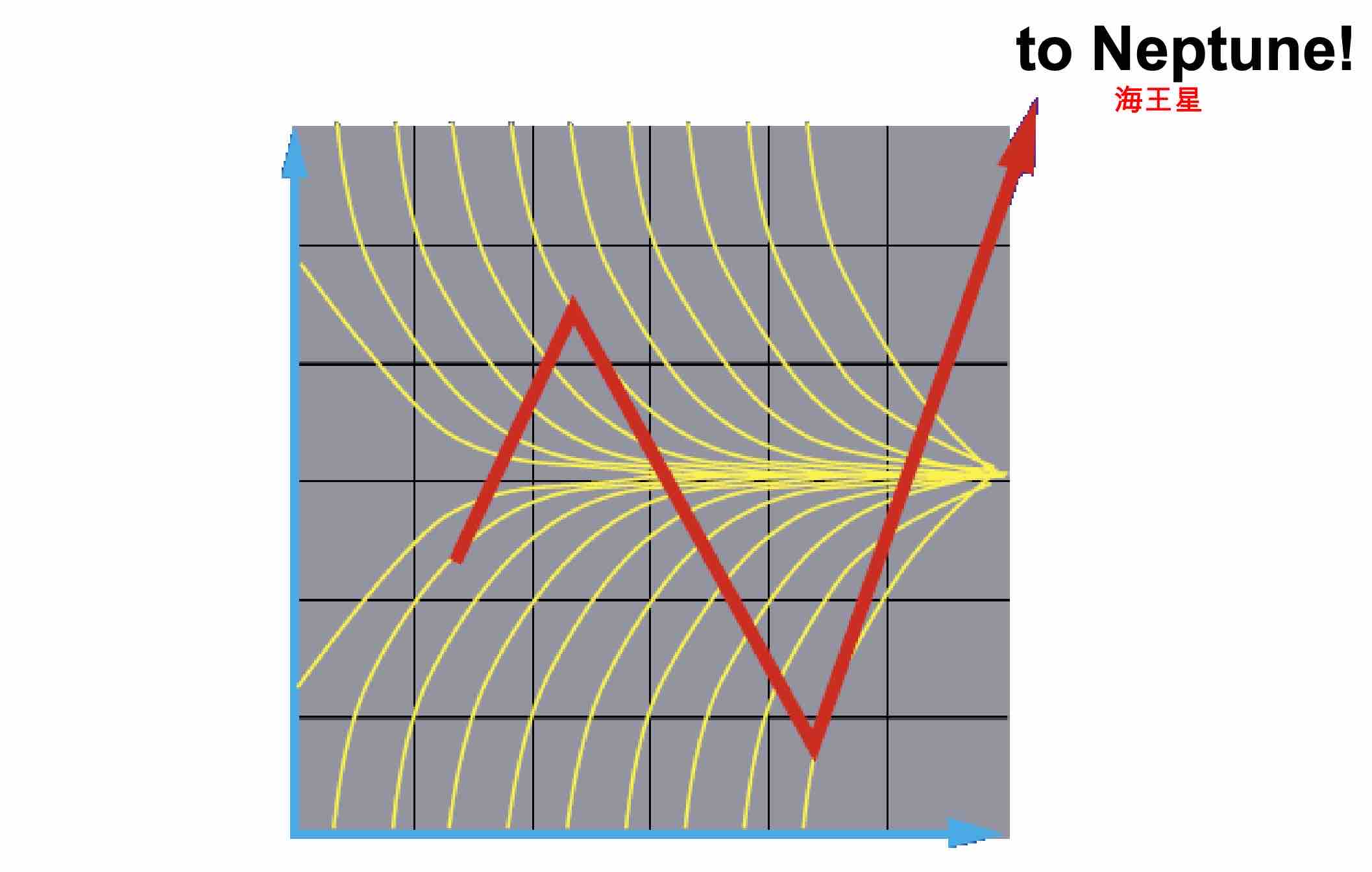
所以我们要对欧拉方法进行修正 The Midpoint Method 推导过程见wiki

1 Compute an Euler step

2 Evaluate f at the midpoint

3 Take a step using the midpoint value

总结一下：欧拉方法是一阶的，中点法是二阶的；这两种方法都很基础，不要用欧拉法因为它很不好，更多方法见 Numerical Recipes

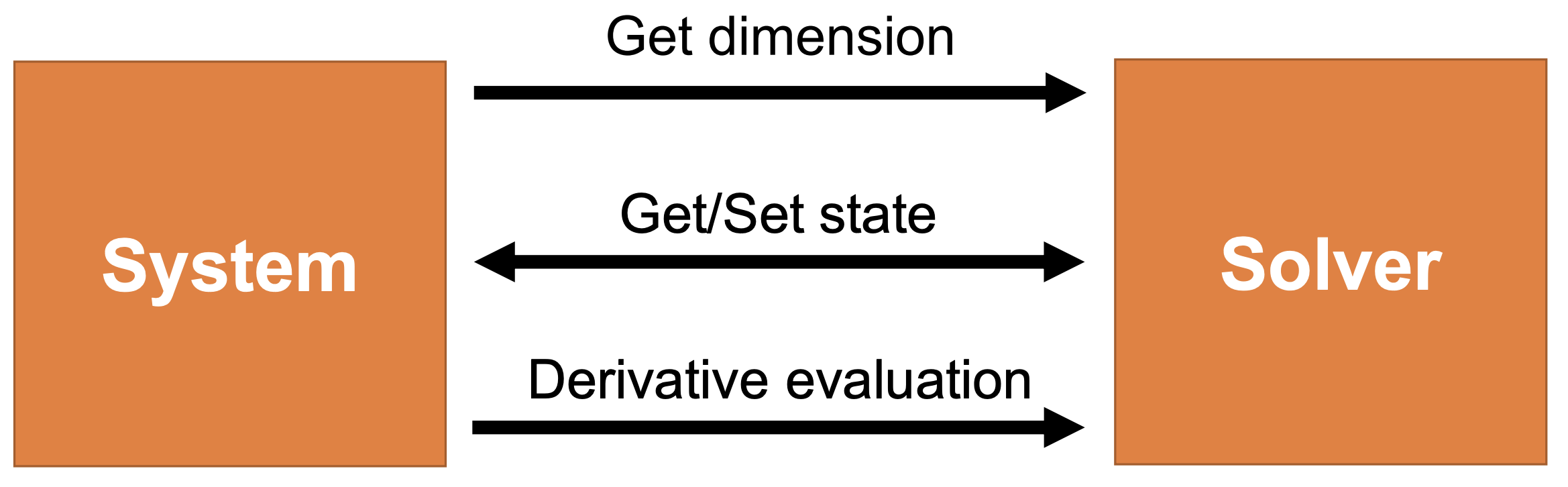
Modular Implementation

Solver Interface