课程 图形学 Sampling & Aliasing
about 图形学的采样和混叠。
属于图形学系列文章。
Analog signal (可以用一个函数表示,连续的) vs Digital signal (离散的)
reconstruct from digital signal -> sampling rate
Nyquist Rate
Aliasing 采样率不够导致的问题 jagged(锯齿状的) or staircase effect
sinusoids function:Any signal can be expressed as a sum of sinusoids of different frequencies (A + Φ)
Spectral Analysis 将复杂信号分解为较简单信号的技术。许多物理信号均可以表示为许多不同频率简单信号的和。找出一个信号在不同频率下的信息(如振幅、功率、强度或相位等)的做法即为频谱分析。from 百度百科
Fourier transform
频谱(spectral) 是指一个时域的信号在频域下的表示方式,可以针对信号进行傅里叶变换而得,所得的结果会是分别以幅度及相位为纵轴,频率为横轴的两张图。from 百度百科
高频决定细节部分,低频决定总体形状。 Lower frequencies -> lower sampling rate -> lower number of pixels, lower resolution
Amplitude: How much details?
Phase: Where are the details?
Q: 如何 Reducing Frequency Content?
A: Filtering - Applying mathematical function (e.g. Averaging pixels (Box Filter)) over a window around every pixel
更复杂的方法就是函数选择复杂一点的,或者选择多个窗口滤波
Why prefiltering helps?见下图
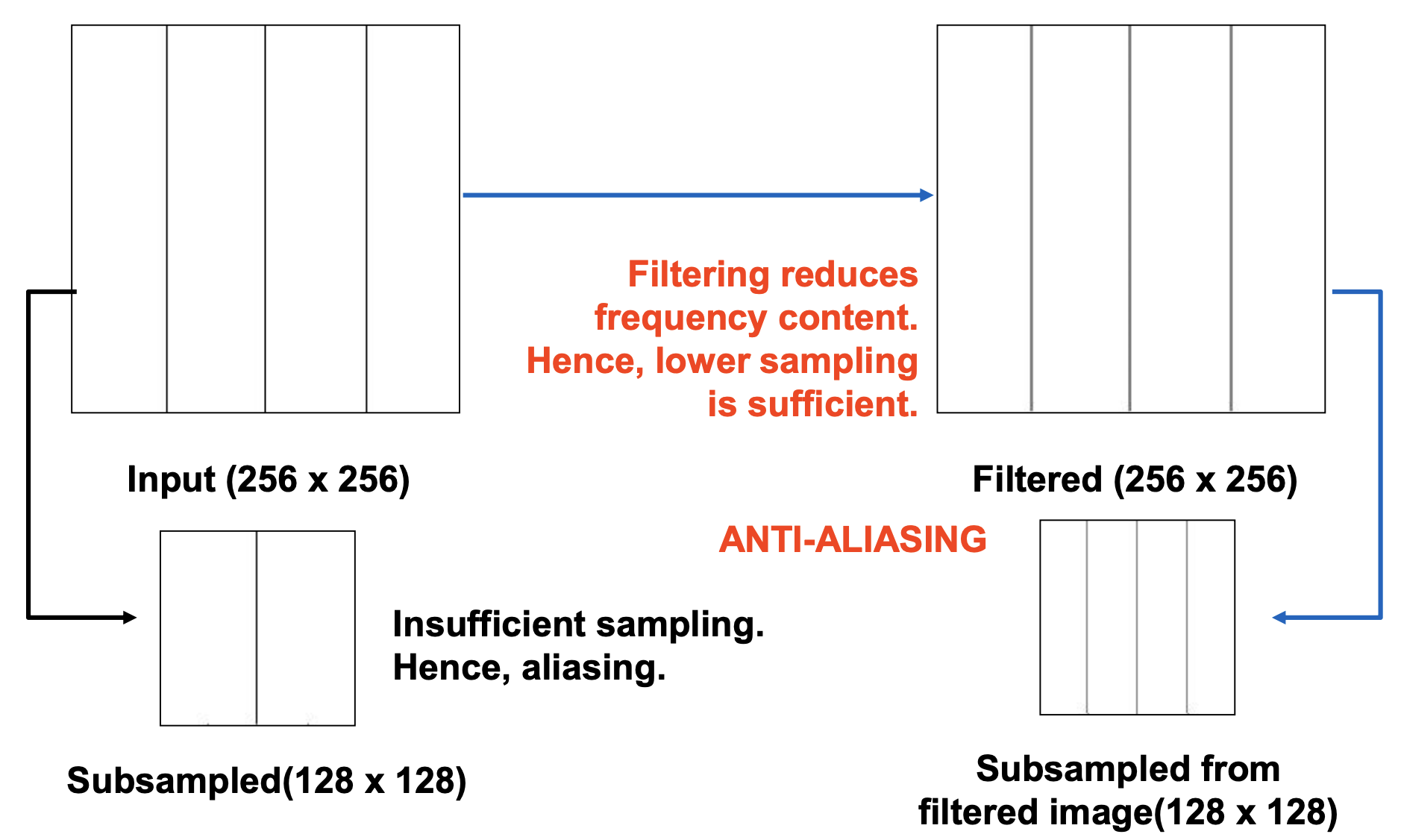
【题外话】给定经过变换和投影之后的顶点,颜色以及纹理坐标,给每个像素(Pixel)正确配色,以便正确绘制整幅图像。这个过个过程叫光珊化(rasterization)或扫描变换(scan conversion),即从二维顶点所处的屏幕空间(所有顶点都包含Z值即深度值,及各种与相关的着色信息)到屏幕上的像素的转换。
Aliasing in Scan Conversion
最好的避免锯齿的方法是要有足够大的采样频率,但多数情况下这个条件无法满足。我们用其它技术来解决这个问题。
方法1: Supersampling and Filtering 也就是 Postfiltering
count the number of sub pixels overlapped by line
超采样:原来一个像素点直选1个样本,现在一个选择多个样本。如下图示意,这里一个像素点选取了9个采样点,我们看左边这9个采样点,直线穿过4个小正方形,最终的颜色=(4⁄9*线的颜色+5⁄9*线外的颜色)。

方法2: Area Averaging 也就是 Prefiltering
count % of area of pixels overlapped by line (gray value)
这两个方法都很 Expensive,对于 offline rendering applications 很常见。
参考:
2.youtube
Aliasing during z-buffering
三个对象共享一个像素点,产生 Z intersection,只有最前面的元素被渲染。
解决方法:Area weighted average
Temporal Aliasing Animation
Speed of the object too fast
Jittered Motion 抖动运动
参考:
1.wiki
2.youtube