特长，知识点特多，适合哪里不会查哪里。

Topics

What topics have I learned so far? 摘自课程主页

一、Cryptography: History and Simple Encryption Method

Topics: Historical Ciphers, Crypto Terminology

二、Encryption

Topics: Symmetric/Convential vs. Public Key Cryptograpy, Block Ciphers, DES, Other Symmetric Ciphers, AES/Rijndael, OTP (Refresher)

三、Cryptographic Hash Functions

Topics: Cryptographic Properties, Simple Hash Functions, MD5, SHA, HMAC

四、Some “fun” math

Topics: Groups, Rings, Fields, Euclidean Algorithm, Chinese Remainder Theorem

五、Public Key Cryptography

Topics: Diffie Hellman Key Exchange, RSA Encryption, Square-and-Multiply, El Gamal Encryption, Digital Signatures (RSA and El Gamal), Digital Signature Standard (DSS), Identification (Fiat-Shamir), Zero-Knowledge Cave

六、Authentication and Key Distribution

Topics: Definitions, Types of Authentication, Biometrics, Protocols, Key Distribution

内容已转移到另一篇博文

Details

1. cryptography

some concepts：

  • security service
  • security mechanism (e.g. cryptography, system controls os 或者 db, hardware controls smartcards, policies 定期修改密码, physical controls 物理隔绝)
  • security attack (e.g. Interruption, Interception, Modification, Fabrication 分别对应 availability 可获得性, Confidentiality 保密性, Integrity 完整性, Authentication 认证性)
  • 来自外部的攻击：passive threats（数据保密） / active threats（消息认证）
  • 来自内部的攻击：发送方否认 / 接收方否认（数字签名）
  • open / closed design model

Closed design has many benefits. An average attacker that does not have access to the algorithm must start from understanding the algorithm before he/she can attack the system. Understanding the algorithm usually takes a very long time and the attacker must spend a lot of resource to accomplish it.

However, there are cases where the attacker has a lot of time and resources. This might be an adversary that is backed by a large company or even a nation state. Moreover, algorithms might leak for some reason. This is possible, for example, through social engineering or even angry employees that seek revenge. Closed design systems rely on the secrecy of the algorithm, and once leaked, the system is already vulnerable.

In open design, we assume that the adversary already has access to the algorithm. This in itself is already better than the closed design, because we do not have to worry about how resourceful our attackers are. Since open design algorithm assumes adversaries with arbitrary strength, they must rely on math that even the most powerful adversary cannot solve. That is why a lot of the algorithms we see in the class is based on NP-complete problems, which is assumed that there are no algorithm that solves it efficiently.

simple encryption method: shift, affine, substitution, vigenere（生成一列数与message相加）, vernam (one-time-pad 生成一列数与message异或)

A cryptosystem has (at least) :

  • Plaintext
  • Secret Key
  • Ciphertext
  • Encryption Algorithm
  • Decryption Algorithm

Attacks on Classical Cryptography

  • Ciphertext-only attack
  • Known-plaintext attack
  • Chosen plaintext
  • Chosen ciphertext
  • Brute force / 统计分析 / 数学分析

密钥长度与暴力破解时间对照表

Attainable Security

  • Perfect, unconditional or “information theoretic”
  • Reducible or “provable”
  • Ad hoc 只是看起来可行

A cryptosystem with computational security is, for the mean time, unbreakable. It relies on the hardness of a NP-complete problem (such as solving discrete logarithm) to ensure the security of the system. There are no known efficient algorithms that solve such NP-complete problems, but we do not know when it might appear in the future. That is why such system is “for the mean time” unbreakable.

A cryptosystem with information theoretic security is provenly unbreakable. Even if software or hardware mature in the future, such systems will still be unbreakable, unlike computational security.

Proving whether a system is computationally secure or information theoretically secure is way out of what we cover in this course, but I will give you a very simple intuition behind how we can prove it.

To prove whether a system is information theoretically secure, you have to prove that a plaintext will be transformed to any possible ciphertext that is the same length as the plaintext. To achieve that, the plaintext must be encrypted with a key with the same length or larger than the plaintext. Also, the key must be chosen truly random from a given distribution. There is only one cryptosystem that does this, and it is called one-time pad.

To prove whether a system is computationally secure is a little more complex, but to give you an intuition, you can do it by proving that the security of the cryptosystem relies on the hardness of the underlying mathematical problem. This is called “reducing” in cryptography.

If you are interested in learning more about this, you should take a cryptography course.

Computational security 是指破解的开销 > 信息本身的价值 或是 破解花费的时间 > 信息的时效性

kerchkoffs原则 是指加密算法应建立在算法的公开上，并且公开算法不影响明文和密钥的安全

加密算法分类

  • operation type (binary/integer arithemetic)
  • # of keys (对称/非对称)
  • how plaintext is processed (block cipher/stream cipher)

2. symmetric encrption

2.1 特点

  • 缺点: 1. key distribution (secure? efficient?) 2. management problem (remain secret both side) 3. short life time (相对而言)
  • 优点: 1. high data throughput 2. short key size (相对) 3. simple
  • 使用时需注意: 1. meesage transmission (安全的信道) 2. secure storage 3. strong authentication 4. digital sigature (应用)
  • 与非对称加密对比: 非对称加密保密性较好，能持续的时间长，数字签名很高效；但是它的key size很大（相对传统加密算法，RSA有2048位，3-DES有112位，AES有216位）导致运行效率比较低，此外它的运行建立在当前人类算力的基础上，不保证将来是否行得通。

2.2 DES

全称 data encryption standard

2.2.1 Block cipher

Generic Example of Block Encryption

Feistel Cipher Structure

下图为1973年Horst Feistel提出，基本上所有 block encrption 都满足这个框架: 其中算法的安全性由图上4部分决定

block cipher 历史

2.2.2 Basic Structure of DES

For each round, 加密 and 解密:

Key schedule:

Function F:

DES Substitution Boxes Operation:

S盒的例子（摘自引用2）

Operation Tables of DES:

Breaking DES (Cryptanalysis)

Meet-in-the-middle ATTACK

DES Variants

2.3 Modes of Operation

可参考维基百科

2.3.1 “Native” ECB Mode

Electronic Code-Book (ECB) Mode

$$ C_i = E ( K, P_i ) $$
$$ P_i = D ( K, C_i ) $$

特点：

  • 同样的明文会生成相同的加密块，ciphertext 可能存在重复 (same patterns) -> 容易收到 replay 攻击
  • Ciphertext block rearrangement is possible -> block 之间交换不会影响最后的结果，所以需要在 plaintext 中加入 block numbering
  • 加密和解密可以并行化 (random access)
  • Error in one ciphertext block -> one-block loss

2.3.2 CBC Mode

Cipher-Block Chaining (CBC) Mode

$$ C_i = E ( K, P_i ⊕ C_{i-1} ), C_0=IV $$
$$ P_i = D ( K, C_i ) ⊕ C_{i-1} $$

特点：

  • 同样的明文会生成不同的加密块
  • Block rearrangement is detectable -> 因为交换顺序会影响前一个block的cipher
  • 加密无法并行化，但解密可以
  • Error in one ciphertext block -> two-block loss

2.3.3 OFB Mode

Output Feedback (OFB) Mode

$$ C_i = E ( K, V_{i-1} ) ⊕ P_i $$
$$ V_0=IV, . . . ,V_i = E ( K, V_{i-1} ) $$
$$ P_i = E ( K, V_{i-1} ) ⊕ C_i $$

特点：

  • 同样的明文会生成不同的加密块
  • Block rearrangement is detectable
  • Key-stream is independent of plaintext
  • Error in one ciphertext block -> one-block loss
  • One-block ciphertext loss -> big mess
  • Can encrypt less than block size
  • Can be run in parallel if the keystream is pre-computed

2.3.4 CFB Mode Cipher Feedback (CFB) Mode

$$ C_i = P_i ⊕ E (K, C_{i-1}), C_0=IV $$
$$ P_i = E ( K, C_{i-1} ) ⊕ C_i $$

特点：

  • 同样的明文会生成不同的加密块
  • Block rearrangement is detectable
  • Key-stream is dependent of plaintext
  • Bit error in one ciphertext block -> one-bit + one-block loss in plaintext
  • Error in one ciphertext block -> 1-extra-block loss
  • Can encrypt less than block size

2.3.5 CTR Mode

Counter (CTR) Mode

$$ C_i = E ( K, CTR ) ⊕ Pi, CTR ++ $$
$$ P_i = E ( K, CTR ) ⊕ C_i $$

特点：

  • Duplicate plaintext blocks (patterns) NOT exposed, unless?
  • Block rearrangement is detectable
  • Key-stream is independent of plaintext
  • 加密和解密可以并行化 (random access)
  • Bit error in one ciphertext block -> one-bit error in plaintext
  • One-block ciphertext loss -> big mess (I think this is assuming that the receiver does not know which ciphertext block was lost. In that case he does not know which index needs to be skipped for decryption and so all the blocks after the lost block will be decrypted to garbage since their index is shifted by the number of blocks lost)
  • Can encrypt less than block size

2.3.6 MAC Mode

Message Authentication Code (MAC) Mode

$$ C_i = E ( K, P_i ⊕ C_{i-1} ), C_0=IV $$

What is sent or stored: $$P1, …, Pn$$, $$Cn = MAC$$

Receiver recomputes Cn with K and compares

特点：

  • Encryption is the same as in CBC mode, but, ciphertext is NOT sent!
  • Any change in plaintext results in unpredictable changes in MAC

Q: DIfference between CBC mode and MAC mode

A: First of all, MAC is not a mode of encryption. It stands for “Message Authentication Code” and it is used to provide integrity to the sent message.

Here is how it works:

Let’s assume that Alice wants to send message M to Bob. If she sends only M to Bob, then Eve can easily modify M to M’.

So, to prevent that from happening, Alice calculates MAC of M and sends both M and its MAC to Bob.

Bob can recalculate the MAC from the received M and crosscheck with the one he received from Alice. If they match, there was no tampering 篡改 to M.

Here is how Bob can recompute MAC:

Both Alice and Bob negotiate on what kind of MAC calculation algorithm they are both going to use before Alice sends the message to Bob.

Recall that in computer security, algorithms are not secret (this is called open design). Therefore, Alice and Bob both know how to use the algorithm.

2.3 AES

  • Advanced Encryption Standard - The Rijndael Block Cipher
  • 为找到DES的替代方案，NIST (美国国家标准与技术研究院) 发起了竞赛，要求
    • Symmetric-key ciphers supporting 128, 192, and 256 bit keys
    • Royalty-Free
    • Unclassified (i.e., public domain)
    • Available for worldwide export
  • 其中第一名是 Rijndael
  • Allows only 128, 192, and 256-bit key sizes (unlike other candidates)
  • Variable input block length: 128, 192, or 256 bits. All nine combinations of key-block length possible.
  • Vast speed improvement over DES in both hw and sw implementations
    • 8,416 bytes/sec on a 20MHz 8051
    • 8.8 Mbytes/sec on a 200MHz Pentium Pro

关于 implement 上相对DES的提升：

  • Well-suited for software implementations on 8-bit processors (important for “Smart Cards”)

    • Atomic operations focus on bytes and nibbles, not 32- or 64-bit integers
    • Layers such as ByteSub can be efficiently implemented using small tables in ROM (e.g., < 256 bytes).
    • No special instructions are required to speed up operation, e.g.,barrel-shifting registers on some embedded device microprocessors

  • For 32-bit implementations:

    • An entire round can be implemented via a fast table lookup routine on machines with 32-bit or higher word length
    • Considerable parallelism exists in the algorithm
    • Each layer of Rijndael operates in a parallel manner on the bytes of the round state, all four component transforms act on individual parts of the block
    • Although the Key expansion is complicated and cannot benefit much from parallelism, it only needs to be performed once when the two parties switch keys

  • Hardware Implementations

    • Rijndael performs very well in software, but there are cases when better performance is required (e.g., server and VPN applications).
    • Multiple S-Box engines, round-key XORs, and byte shifts can all be implemented efficiently in hardware when absolute speed is required
    • Small amount of hardware can vastly speed up 8-bit implementations

  • Inverse Cipher

    • Except for the non-linear ByteSub step, each part of Rijndael has a straightforward inverse and the operations simply need to be undone in the reverse order.
    • However, Rijndael was specially written so that the same code that encrypts a block can also decrypt the same block simply by changing certain tables and polynomials for each layer. The rest of the operation remains identical.

3. hash

3.1 Cryptographic Hash Functions

  • 缩写：CHF
  • 优秀的密码学hash函数性质 ( ✅表示本身hash function就具有的功能 )
    1. Takes on input of any size ✅
    2. Produces fixed-length output ✅
    3. Easy to compute (efficient) ✅
    4. Given any h, computationally infeasible to find any x such that H(x) = h ➡️ One-Way-ness
    5. For a given x, computationally infeasible to find y: H(y) = H(x) and y≠x ➡️ Weak Collision-Resistance
    6. Computationally infeasible to find any (x, y) such that H(x) = H(y) and x ≠ y ➡️ Strong Collision-Resistance

3.2 Merkle-Damgard construction

  • compression function f(): fixed-size

3.3 Birthday Paradox

How long should a hash be?

个人认为这里的1/2是根据上面的图估计出来的，详情见论文 Hash Function Balance and its Impact on Birthday Attacks

3.4 CHF from a Block Cipher

  1. Split input into a sequence of keys: M1,…Mp
  2. Encrypt a constant plaintext (e.g., block of zeros) with this sequence of keys: Hi = E ( Mi, Hi-1 ), H0= 0
  3. Final ciphertext Hp is the hash output

Davies-Meyer CHF 加密方程为异或⊕

3.5 Hash Func Examples

Latest standard: SHA-3

  • 仍然是 NIST (美国国家标准与技术研究院) 发起的一场竞赛，07年开始征求协议，08年有51份提交，09年14份进入半决赛，最后10年5份决赛，最终的胜出者是 Keccak

  • Designed by Bertoni, Daemen, Peeters, Van Assche.

  • Based on “sponge construction” 海绵函数, a completely different structure from prior CHF-s.

3.6 Message Authentication

哈希函数除了能保证消息的完整性，还能应用于 Message Authentication：

下面那种方法比上面的更简单，不需要加密解密，只需要比较哈希值就行。我原来注明了它是Challenge-response authentication 但其实不太一样，后者更加复杂，详见链接。

3.7 HMAC

  • Just computing and appending H(m) to m is enough for integrity but not for authenticity 这句话意思是我们将哈希后得到的 message digest 附在原来的 message 后面只能用作验证文本的完整性，但我们无法用来验证身份。我们需要一个“Keyed Hash”

算法流程

4. asymmetric encryption [四、五]

4.1 Number Theory

4.1.1 判断有限代数结构（Finite Algebraic Structures）

  1. Group (G,@): closure / associativity / identity / inverse
  2. Abelian 阿贝尔群/交换群: commutativity
  3. Cyclic: group generator G=<g>
  4. Order of a group: the size of set G |G| or #{G} or ord(G)
  5. Group (G,@) is finite if ord(G) is finite
  6. Rings (R, +, *)： (R, +) is an Abelian group (identity=0) & closure / associativity / identity=1 / distribution
  7. Monoid: associative / identity
  8. Fields (F, +, *): Commutative Ring + Inverse(*)
  9. Subgroup (G,@): H is a subset of G & (H, @) is a group

Some cases hard to understand:

  1. Integers mod(p) (where p is Prime) under Multiplication -> Nonzero integers mod p -> 这个集合包含所有模p等于1,2,…,(p-1)的数
  2. non-zero integers mod N = {1 …, x, … n-1} such that GCD(x, N)=1 -> 这个集合包含所有模n等于1,2,…,(n-1)的数，和前一个的区别在于这里 N 不一定是质数，任何数都可以

4.1.2 extended euclidian algorithm

4.1.3 chinese remainder theorem(CRT)

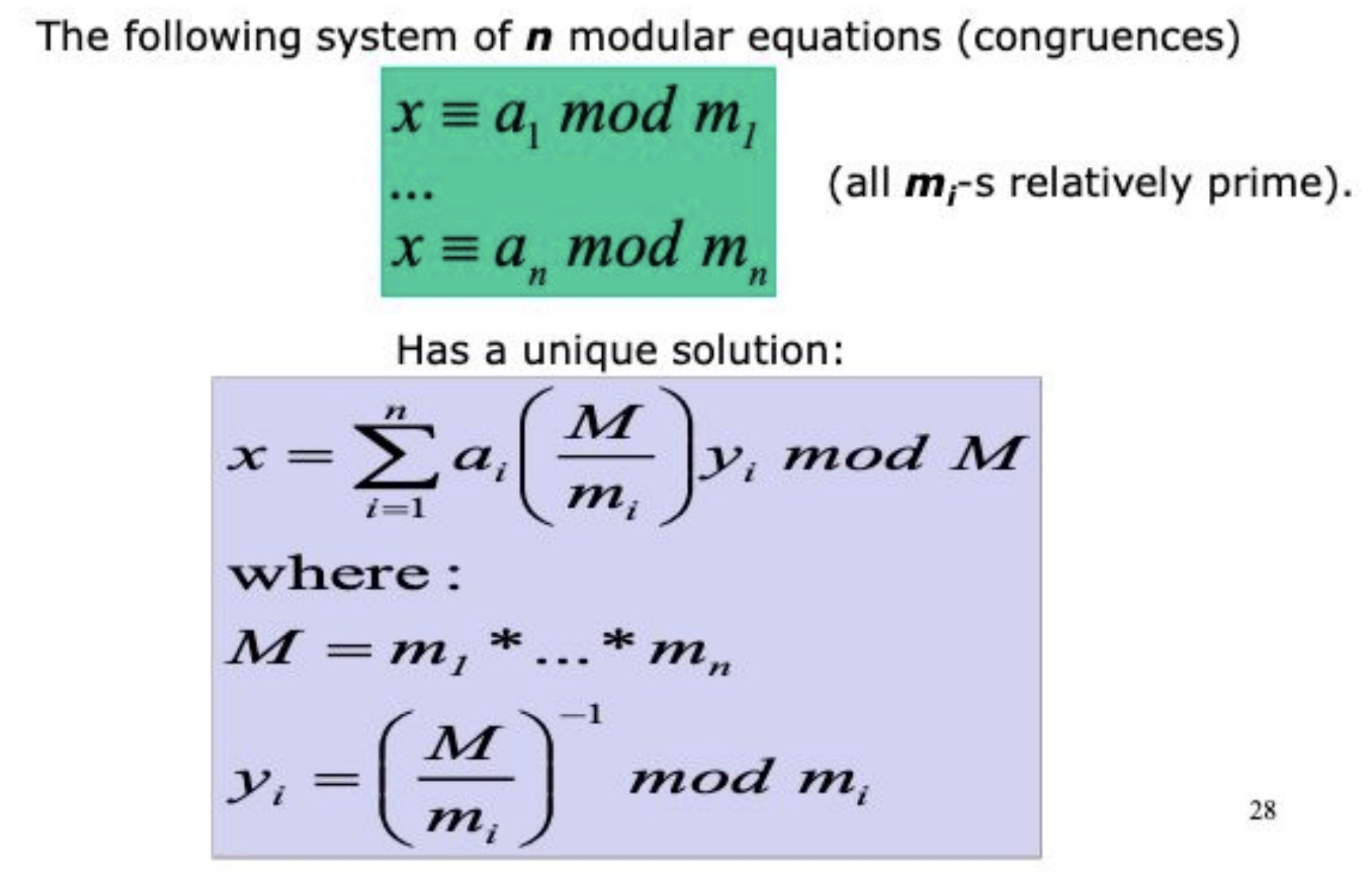
4.2 Asymmetric Cryptography

  • 也叫 Public Key Cryptography
  • 优点：no key distribution problem
  • 缺点：slow (对称 - bitwise operation / 非对称 - multiplication, exponentiation and modular arithmetic)
  • Encryption done with public key, decryption done with private key
  • Digital signatures
    • Signing done with private key, verification done with public key
    • Signature is encryption of message hash and provided along with the message 【Q:所以说传递的信息为：原信息+原信息哈希后经过加密的签名？A:发送报文时，发送方用一个哈希函数从报文文本中生成报文摘要,然后用对方的公钥对这个摘要进行加密，这个加密后的摘要将作为报文的数字签名和报文一起发送给接收方，接收方首先用与发送方一样的哈希函数从接收到的原始报文中计算出报文摘要，接着再用接收方的私钥来对报文附加的数字签名进行解密，如果这两个摘要相同、那么接收方就能确认该数字签名是发送方的。(from 百度百科)】
    • Provides authentication (认证，是不是对方发的？), integrity (消息有没有被中间人恶意篡改？), and non-repudiation (不可抵赖的)

4.2.1 Diffie–Hellman key exchange

wiki: 迪菲-赫尔曼密钥交换是一个匿名（无认证）的密钥交换协议。它可以让双方在完全没有对方任何预先信息的条件下 通过不安全信道创建起一个密钥 ，这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。它是很多认证协议的基础，并且被用来提供传输层安全协议的短暂模式中的前向安全性。（后一篇离散数学的post最后部分也关于这个过程的流程图）

当然，所有算法可行的前提是它们的问题是 HARD 的，不属于 P class；有点不理解DH和DDH的区别，这个回答提供了帮助：

此外，Diffie–Hellman只有当攻击者处于监听状态（passive）时才有效，如果你正在和一个伪装成别人的攻击者（active）通信，这种交换协议是无效的。

那有没有可能利用对称加密来交换密钥呢？答案就是 Merkle’s Puzzles (1974) 🔗

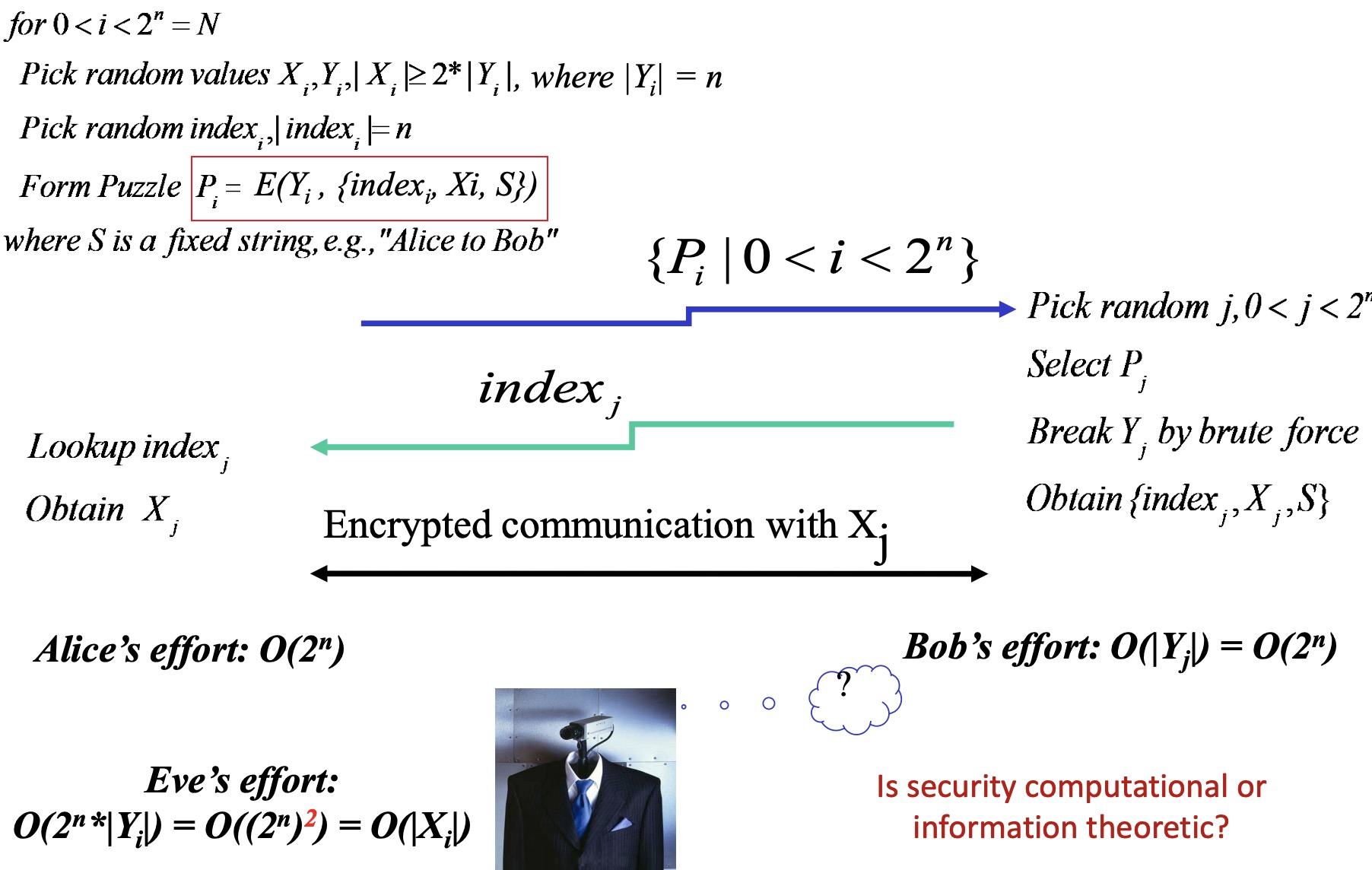
4.2.2 RSA

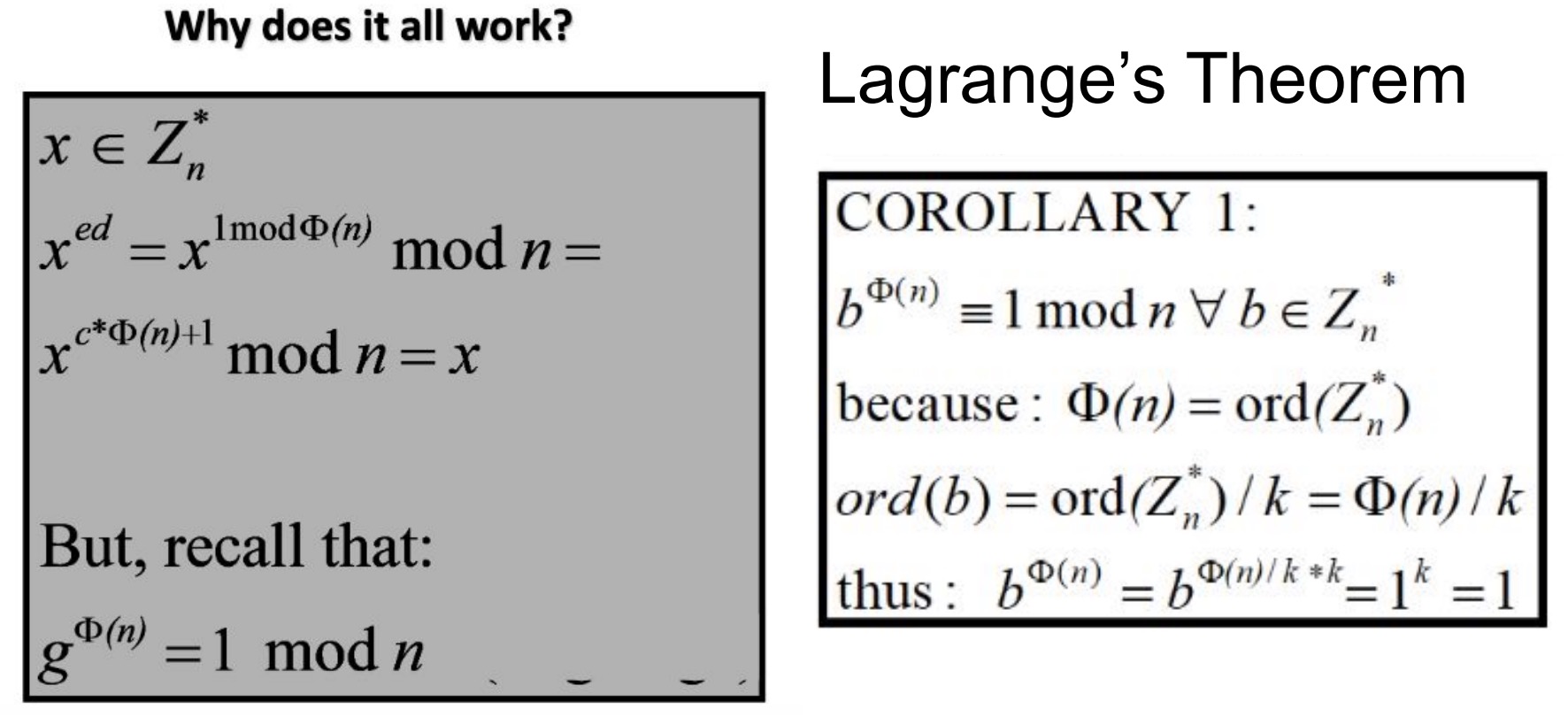
Why does it all work? 在这个地方卡了很久都没看懂想说明什么，严重影响复习效率。后来翻几个推荐的textbook，发现有一本（Network Security: Private Communication in a Public World）刚好能对上。课件拌书食用，效果更佳！

这里是想证明 x^de = x mod n, 所以才可以还原加密的内容。拉格朗日定理是说 for any g in G, ord(g) divides ord(G)，网上没怎么查到这一定理，大概是其它定理更有名？

Why secure?

  • Conjecture: breaking RSA is polynomially equivalent to factoring n

  • Recall that n is very, very large

  • Why: n has unique factors p, q; Given p and q, computing (p-1) (q-1) is easy

    • ed ≡ 1 mod Φ(mn)
    • Use extended Euclidian

复杂度分析

  • 可以参考链接

  • Square-and-Multiply 也叫 快速幂 或 平方求幂 🔗

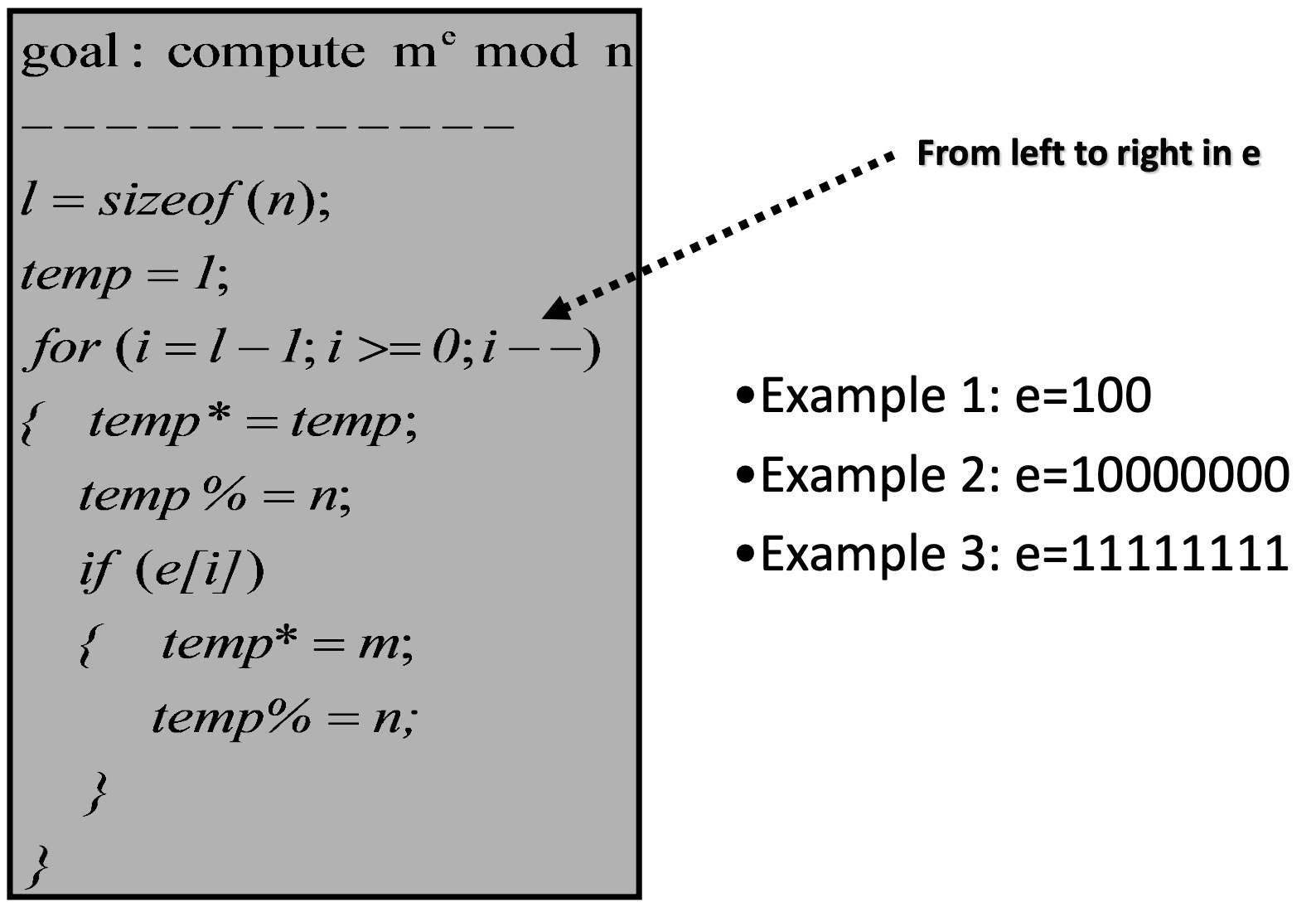
  • Speeding up RSA Decryption 利用中国剩余定理，p、q比n小的多，计算得更快

  • 2 or more parties cannot share the same n

RSA Signature Scheme

  • 这种方法是不安全的

    • In practice, we use a randomized version of RSA (implemented in PKCS#1)
    • Hash the message and then sign the hash

  • The Good:

    • Verification can be cheap (like RSA encryption)
    • Mechanically same as RSA decryption function
    • Security based on RSA encryption
    • Signing is harder but verify-s > 1 …
    • Deterministic

  • The Bad: 🔗 如果不使用HASH函数的后果

    • RSA is malleable: signatures can be “massaged” 交换顺序或者直接扔掉一串
      • m1^d * m2^d = (m1*m2)^d
      • （存在性伪造）使用“已知消息攻击” 拼接之前的签名
      • （选择性伪造）利用“选择消息攻击” 请求多个签名拼接
    • Phony “random” signatures 任何人都能提供随机选择 y, 并计算 m = y^e mod n 来伪造签名者对随机消息m的签名
    • compute Y=RSA(e,X)=X^e mod n
      • X is a signature of Y because Y^d=X mod n
      • 唯密钥攻击的存在性伪造
    • 解决措施就是引入哈希函数，使得消息包含足够多的多余度

  • The Ugly:

    • Signing requires integrity!
    • How to sign multiple blocks when m > n?
    • Deterministic – needs additional randomization!

4.2.3 El Gamal

  • The good:
    • Signing is cheap(er)
    • Designed as a signature function
    • Non-deterministic (randomized)
  • The bad:
    • Need GOOD source of random numbers
    • Randomizers cannot be revealed (trace)
    • Randomizers cannot be reused

4.2.4 The Digital Signature Standard (DSS)

  • Why DSS
    • RSA issues: patents, malleability, etc.
  • A variant of El Gamal, but better performance
  • Originally for |p|=512 bits, now up to 1024
  • Optimized for signature size (320- vs. 1024-bit)
  • Signing - 1 exp, 1 inv, verification - 2 exps, 1 inv
  • No attacks thus far 左边是EI，右边是DSS

4.2.5 Zero-knowledge proof

  • prove ownership of a secret without revealing any info about the secret

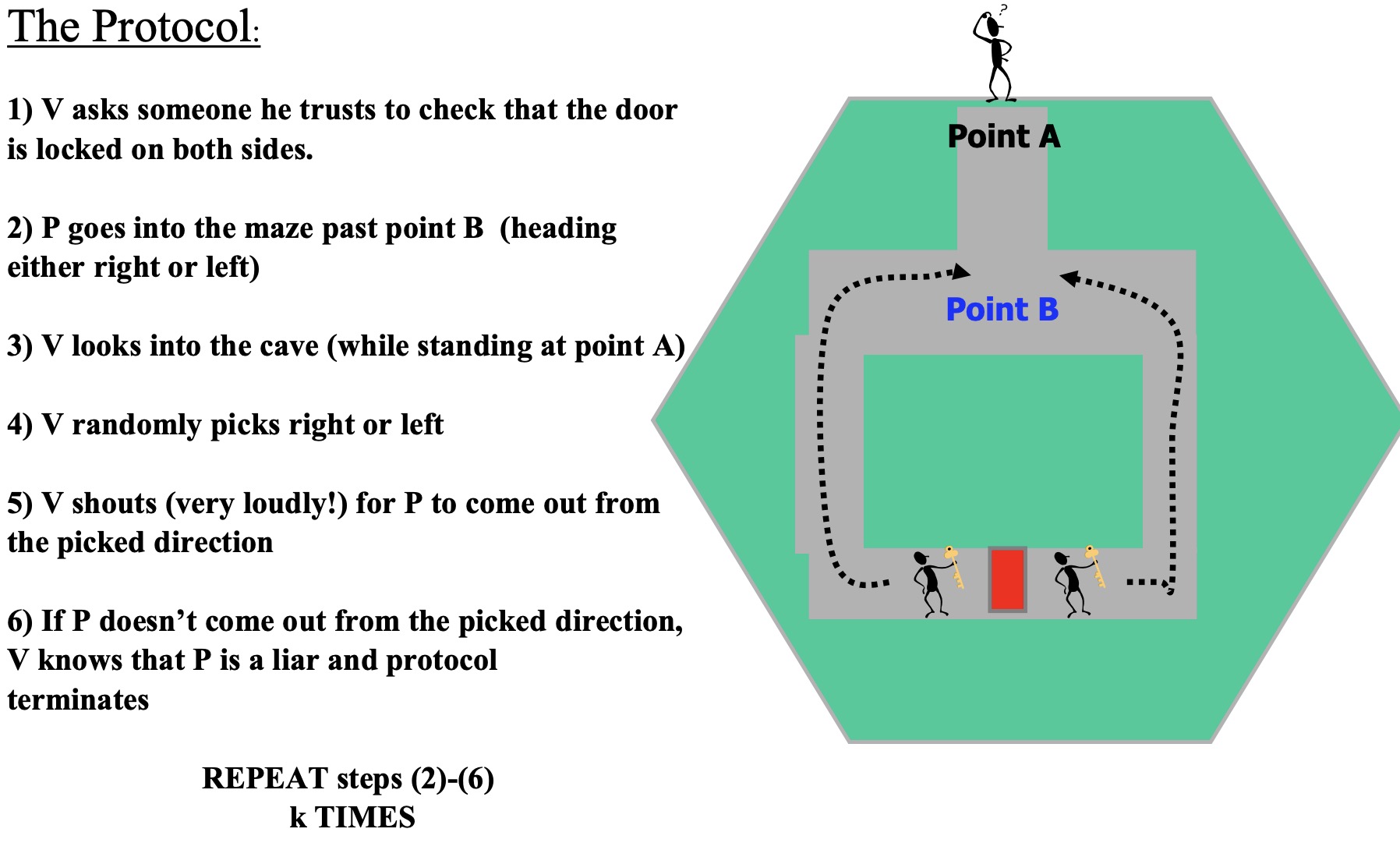
4.2.6 Fiat-Shamir Identification Scheme

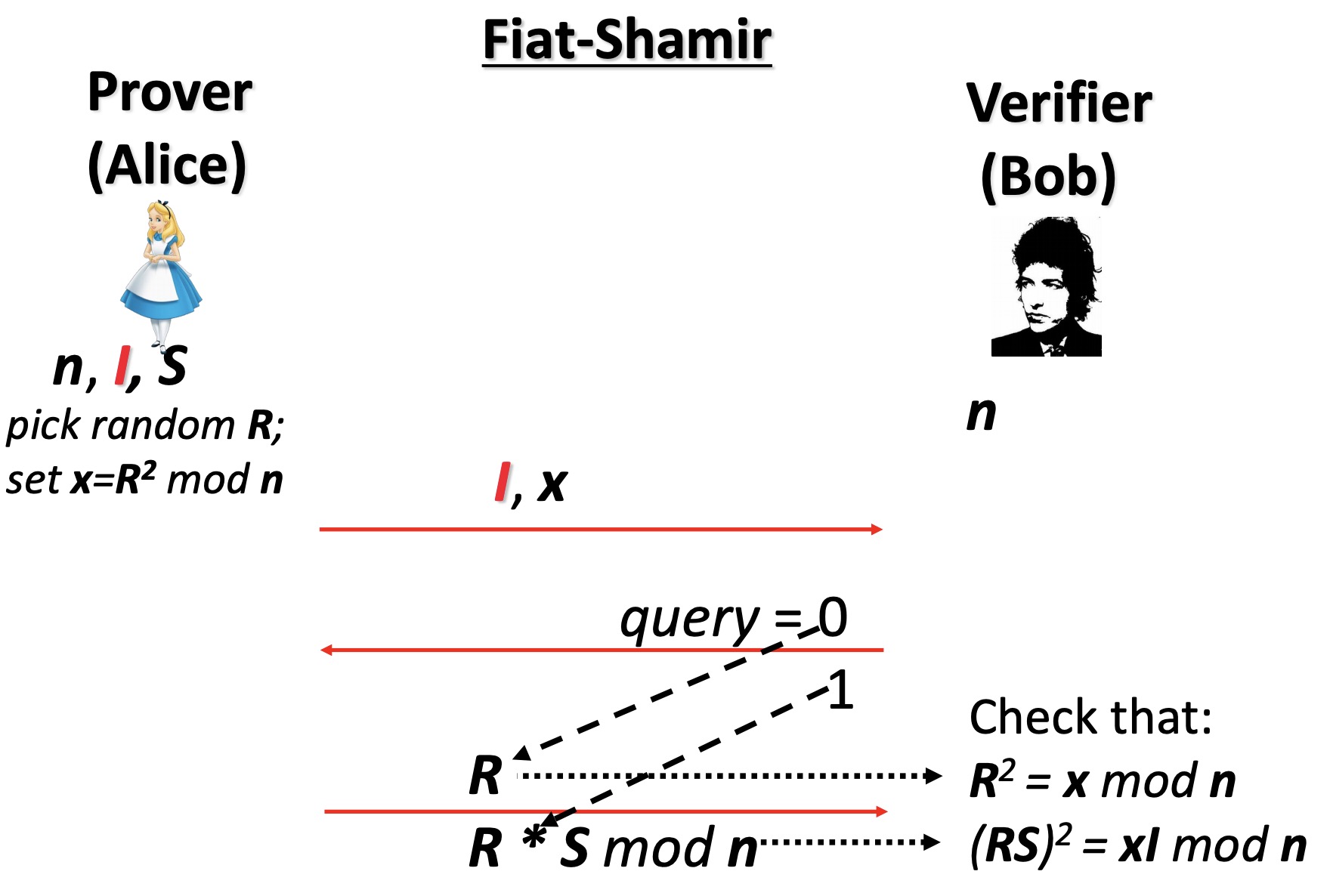Protocol is repeated t (usually 20, 30, or log n) times, and, if each one succeeds, V concludes that P is the claimed party.

What if Prover knows the challenge ahead of time?

⚠️这两个 x 的计算是不一样的，也就是说攻击者无法同时得出两种值（没看仔细研究了好久，还以为这个算法有漏洞…)

CLAIM: Protocol does not reveal ANY information about S

  • The Fiat-Shamir protocol is ZERO-KNOWLEDGE

安全性分析

  • Clearly, if P knows S, then V is convinced of P’s identity
  • If P does not know S, it can either:
    • know R, but not RS mod n. Since P is choosing R, it cannot multiply it by the unknown value S
    • choose RS mod n, and thus can answer the second question: RS mod n. But, in this case, P cannot answer the first question R, since to do so, needs to divide by unknown S
  • In any case, adversary cannot answer both questions, since otherwise he can compute S as the ratio between the two answers.
  • But, we assumed that computing S is hard, equivalent to factoring n.
  • Since P does not know in advance (when choosing R or RS mod n) which question that V will ask, he cannot foresee the required choice. He can succeed in guessing V’s question with probability 1⁄2 for each question.
  • The probability that V fails to catch P in all runs is thus: 2^(-t)
    • e.g., 1 in 1,000,000,000 for t=20

Reference

  1. UCI CS134 课件（mainly）
  2. 现代密码学复习要点总结（谷利泽）